What is the Horizontal Pressure Gradient Error?
DSI has developed animproved version of the EFDC code to help deal with pressure gradient errorsthat occur in simulations that have steep changes in bed elevation. This new version of the code is called the Sigma-Zed code (SGZ) and has been integrated into the EFDC+. Sigma-Zed contrasts with the conventional EFDC approach which applies a sigma coordinate (SIG) transformation in the vertical direction and uses the same number of layers for all cells in the domain. To accommodate the varying depths over the model domain, the thickness of the layers vary from cell to cell but the number of layers and fraction of depth for each layer are constant. This approach introduces a well-known error in the density gradient terms, otherwise known as the pressure gradient error (Mellor, et.al. 1994). These errors are most pronounced in regions with steeply varying bathymetry.
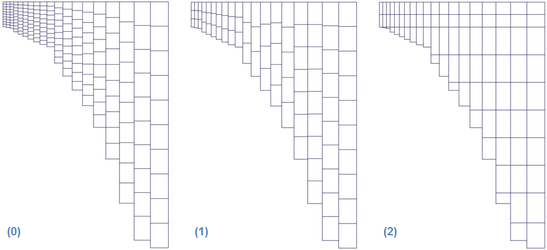
Sigma-Zed Solution to the Pressure Gradient Error
A new vertical layering approach which iscomputationally efficienthas been developed and applied to the EFDC model, therebyreducing these pressure gradient errors.In the Sigma-Zed model, the vertical layering scheme has been modified to allow for the number of layers to vary over the model domain. Each cell can use a different number of layers, though the number of layers for each cell is constant in time. As with the SIG approach, the thickness of each layer varies in time to accommodate the time varying depths. The z coordinate system varies for each cell face, matching the number of active layers to the adjacent cells. The new version is computationally more efficient than a similarly configured SIG grid, thus making models with 20 to 50 layers or more practical for typical projects.
Applications of Sigma-Zed
This new approach has been tested and applied in a numberof cases with notable improvement in results. The model has been applied to Lake Washington (Seattle, WA, USA) and Lake Mead (Nevada, USA), both of which have steep bottom gradients and sharp thermoclines. The results indicate that the vertical variation of temperature and the thermal stratification are accurately reproduced and provide a significant improvement compared to the earlier sigma coordinate transformation method.